Study of pressure head variation of flow over ogee weir

2.     Study of pressure head variation of flow over ogee weir

2.1.       Objectives

1. To study pressure head variation of flow at different sections of ogee weir.
2. To study pressure head variation of flow at different sections of ogee weir by changing flows.

2.2.       Apparatus

1. Ogee weir
2. Point gauge
3. S6 tilting flume assembly

2.3.       Related theory

2.3.1.       Ogee spillway

Ogee spillway is widely used with concrete, masonry, arch and buttress dams. Such a spillway can be easily used on valleys where width of the river is sufficient to provide the required crest length and the river bed below can be protected from scour at moderate costs. The profile of this spillway is made in accordance with the shape of the lower nappe of a freely falling jet, over a duly ventilated sharp crested weir as shown in figure 2.1.

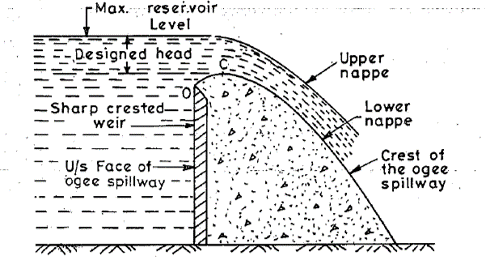
Figure 2.1: section of an ogee spillway with vertical U/S face

The shape of the lower nappe of freely falling jet over a sharp crested weir can be determined by the principle of projectile. It generally rises slightly (to point C) as it originates from the crest (O) of a sharp crested weir and then falls to make a parabolic form. Now, if the space between the sharp crested weir and lower nappe is filled with concrete or masonry, the weir so formed will have a profile similar to an ‘ogee’ (S shaped curve in section) and hence called an ogee weir or an ogee spillway. This lower nappe will then become the crest of the spillway. Since the lower nappe of the freely falling jet will be different for different heads over the crest of the sharp crested weir, the profile of the ogee weir is generally confined to the lower nappe that would be obtained for maximum head over the spillway.

2.3.2.        Cavitation

The crest of the ogee spillway can be made to conform only to one particular nappe that would be obtained at one particular head. This head is called the designed head and represented by H_d but in practice, the actual head of water on the spillway crest, called the operating head, may be less or more than the designed head. If this operating head on the spillway is more than the designed head, the lower nappe of the falling jet may leave the ogee profile thereby generating negative pressure at the point of separation. The generation of vacuum or negative pressure may lead to formation of bubbles or cavities in the water. These cavities or bubbles filled with air, vapour and other gases are formed in a liquid, whenever the absolute pressure (atmospheric pressure-vacuum pressure) of the liquid is close to its vapour pressure, so as to commence evaporation. Such a condition may arise when the head of water is more than the designed head and the consequent high velocity jet causes reduced pressures or negative pressures in the lower region of the water jet.

Such cavities on moving downstream may enter a region where the absolute pressure is much higher (i.e. more vacuum). This causes the vapour in the cavity to condense and return to liquid with an implosion or collapse of the cavity. When the cavity collapses, extremely high pressures are generated. The continuous bombardment of these implosions will thus take place near the surface of the spillway, causing fatigue failure of its material. The small particles of concrete or masonry are this broken away, causing formation of pits on its surface and giving the surface a spongy appearance. This damaging action of cavitation is called pitting. The cavitation plus the vibrations from the alternate making and breaking of contact between the water and face of the spillway, may thus result in serious structural damages to the spillway is more than the designed head, cavitation may occur. On the other hand, if the head of water over the spillway is less than the designed head, the falling jet would adhere to the crest of the ogee spillway, creating positive hydrostatic pressures and thereby reducing the discharge coefficient of the weir.

2.4.       Procedure

1. Set the slope of S6 tilting flume to zero.
2. Attach the ogee spillway to the tilting flume
3. Attach the pipes from ogee spillway to the piezometers.
4. Turn the pump on and note the differential manometer readings to compute the discharge.
5. Note the piezometric values for particular discharge for all the tapings.
6. Repeat the above procedure for various discharges
7. Plot graph between various discharges and pressure heads at different tappings.

(a)

(b)

(c)

Figure 2.2: (a) Piezometers (b), (c) Ogee spillway with marked taping numbers

2.5.       Observations and calculations

2.5.1.       Relation between pressure head and various discharges

Least count of piezometer = 5 mm of water
Sr. no.	Δ H	Q	P1	P2	P3	P4	P5	P6	P7	P8
	mm	m3/s	mm	mm	mm	mm	mm	mm	mm	mm
1	0	0	240	220	235	233	234	224	208	172
2	5	0.002828	251	236	244	238	237	227	210	173
3	15	0.004898	250	232	240	236	237	227	210	172
4	25	0.006323	245	226	235	232	233	226	210	173
5	35	0.007481	240	221	230	227	229	224	210	173
6	45	0.008483	232	211	221	219	223	221	210	173
7	55	0.009378	232	211	221	218	223	220	210	173

 

Sr. no.	Q	P1	P2	P3	P4	P5	P6	P7	P8
	m3/s	mm	mm	mm	mm	mm	mm	mm	mm
1	0	0	0	0	0	0	0	0	0
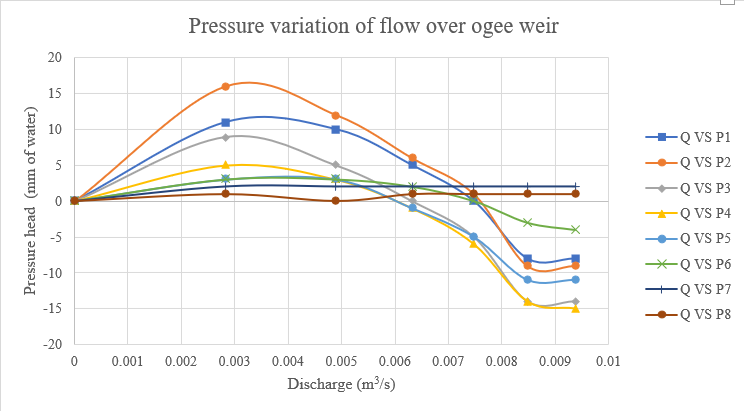
2	0.002828	11	16	9	5	3	3	2	1
3	0.004898	10	12	5	3	3	3	2	0
4	0.006323	5	6	0	-1	-1	2	2	1
5	0.007481	0	1	-5	-6	-5	0	2	1
6	0.008483	-8	-9	-14	-14	-11	-3	2	1
7	0.009378	-8	-9	-14	-15	-11	-4	2	1

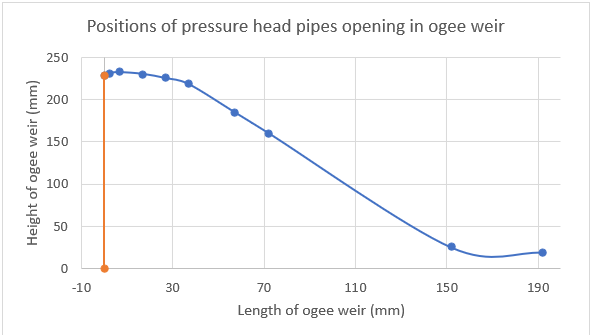
2.5.2.       Position of pressure head pipes in ogee spillway

Pipe #	Horizontal axis	Height	Width
	mm	mm	mm
1	5238	228	0
2	5240	231	2
3	5245	232	7
4	5255	230	17
5	5265	225	27
6	5275	218	37
7	5295	185	57
8	5310	160	72
	5390	25	152
	5430	19	192

2.5.3.       Variation of static head over ogee spillway with varying discharge

Marking #	Elevation head	Q=0.002828 m3/s		Q=0.004898 m3/s		Q=0.006323 m3/s		Q=0.007481 m3/s		Q=0.008483 m3/s		Q=0.009378 m3/s
		Pressure head	Static head	Pressure head	Static head	Pressure head	Static head	Pressure head	Static head	Pressure head	Static head	Pressure head	Static head
	Mm	mm	mm	mm	mm	mm	mm	mm	mm	mm	mm	mm	mm
1	228	11	239	10	238	5	233	0	228	-8	220	-8	220
2	231	16	247	12	243	6	237	1	232	-9	222	-9	222
3	232	9	241	5	237	0	232	-5	227	-14	218	-14	218
4	230	5	235	3	233	-1	229	-6	224	-14	216	-15	215
5	225	3	228	3	228	-1	224	-5	220	-11	214	-11	214
6	218	3	221	3	221	2	220	0	218	-3	215	-4	214
7	185	2	187	2	187	2	187	2	187	2	187	2	187
8	160	1	161	0	160	1	161	1	161	1	161	1	161

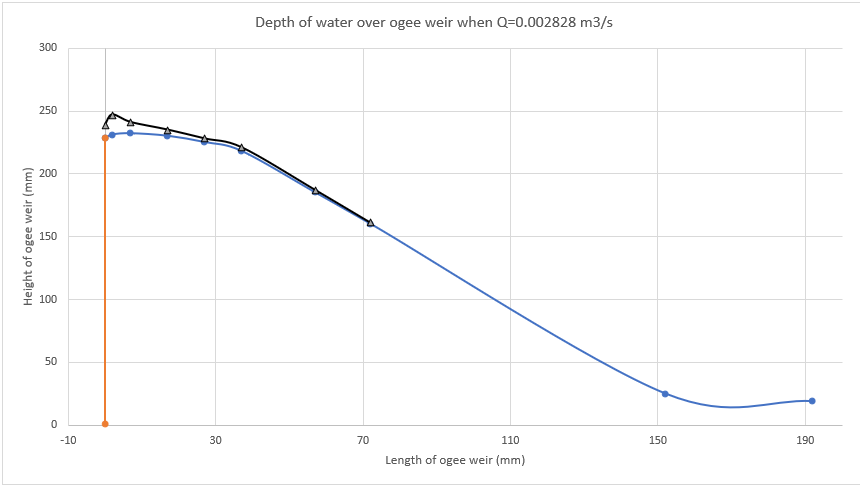
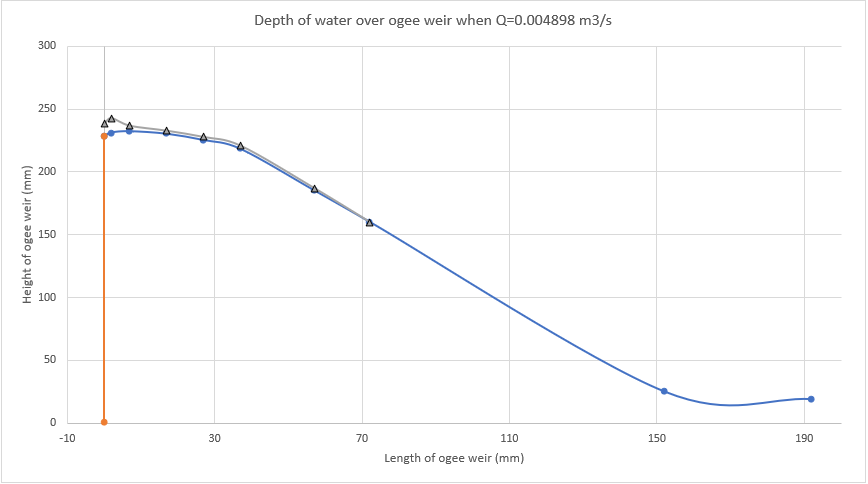
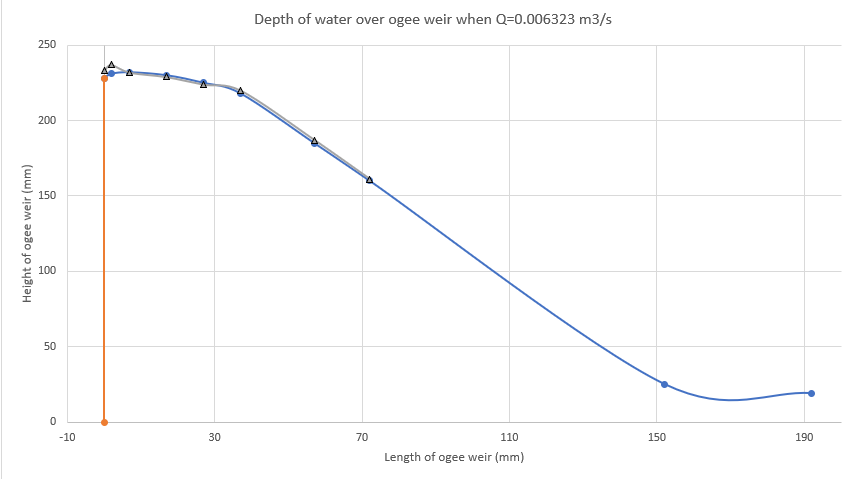
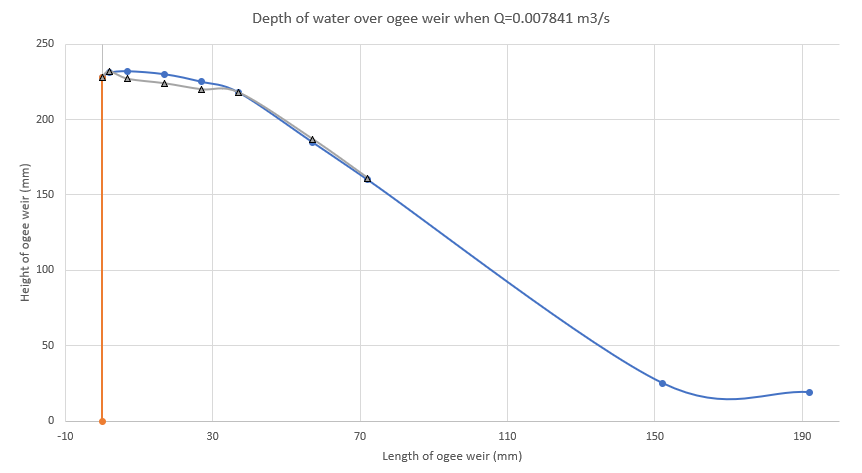
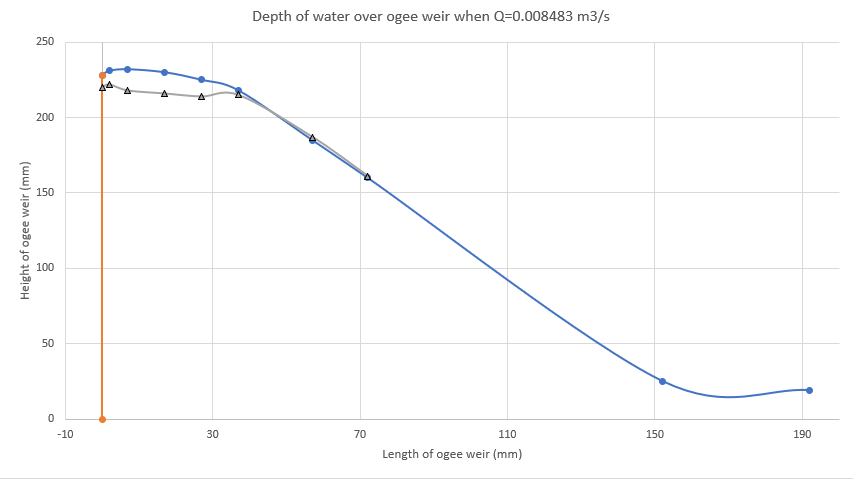
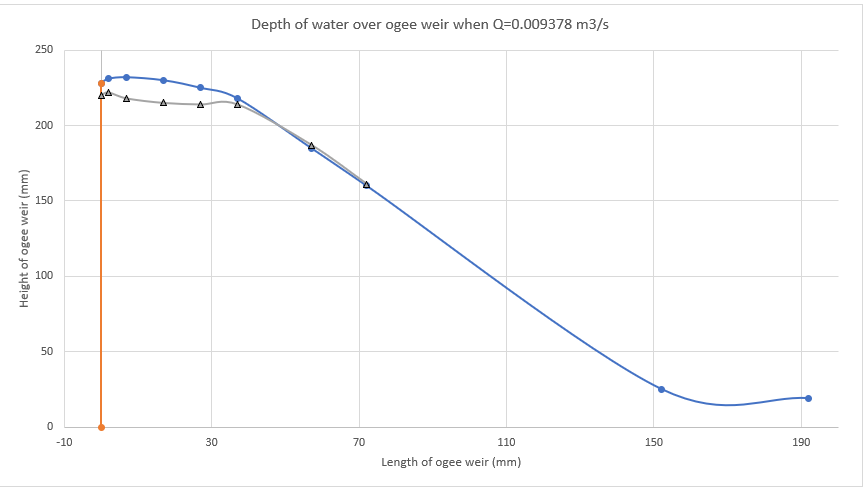
2.6.       Comments

1. At taping number 2, there is more pressure head than that of other tapings.
2. The maximum height of ogee spillway is at taping number 3 and it is 232 mm.
3. With increase in discharge, pressure head is decreasing. The reason is that when there is increase in discharge, the velocity increases. Thus, to satisfy Bernoulli’s theorem, when velocity increases, kinetic energy increases and pressure must be reduced to keep the sun of equation constant. According to Bernoulli’s equation sum of pressure energy, kinetic energy and potential energy must be constant at 2 sections.
4. When velocity of particles of media is quite high, they would be replaced to some other location creating a vacuum at former place, that’s why there is reduction in pressure head when discharge is increased.