Job # 13:
Determination of modulus of rupture of concrete
(ASTM C 78 – 02)
Significance:
- This test method covers the determination of the flexural strength of concrete by the use of a simple beam with third-point loading.
- This test method is used to determine the flexural strength of specimens prepared and cured in accordance with the specifications. Results are calculated and reported as the modulus of rupture.
- The strength determined will vary where there are differences in specimen size, preparation, moisture condition, curing, or where the beam has been molded or swayed to size.
- The results of this test method may be used to determine compliance with specifications or as a basis for proportioning, mixing and placement operations. It is used in testing concrete for the construction of slabs and pavements.
- The modulus of rupture is also used as an indirect measure of the tensile strength of concrete.
Apparatus:
- Mohr and Federhaff Universal Testing Machine
- Supporting Beam and Roller/hinge supports
- Third point loading arrangement
- PCC beams 100mm×100mm×500mm

Mohr and Federhaff UTM
Related Theory:
Difficulties in measurement of tensile strength:
There are considerable experimental difficulties in determining the true tensile strength of concrete. In direct tension test following are the difficulties:
- When concrete is gripped by the machine it may be crushed due the large stress concentration at the grip.
- Concrete samples of different sizes and diameters show large variation in results.
- If there are some voids in sample the test may show very small strength.
- If there is some initial misalignment in fixing the sample the results are not accurate.
Indirect methods for the determination of tensile strength of concrete:
- Split cylinder test
- Double punch test
- Modulus of rupture test
Modulus of Rupture:
For many years, tensile strength has been measured in terms of the modulus of rupture fr, the computed flexural tensile stress at which a test beam of plain beam fractures.
Because this nominal stress is computed on the assumption that concrete is an elastic material, and because this bending stress is localized at the outermost surface, it is larger than the strength of concrete in uniform axial tension.
It is a measure of, but not identical with the real axial tensile strength.
In a flexural test on a plane concrete specimen, the maximum tensile stress reached at the bottom fiber of a standard size prism (beam) under predefined loading type is called modulus of rupture.
Test specifications:
Type/Size of The Specimen for The Test:
The specimen used is a prism, square in cross-section and having a certain length. There are two standard sizes of the specimen that can be used for specified aggregate sizes.
150 x 150 x 750 (mm)
100 x 100 x 510 (mm)
The size (150 x 150 x750 mm) can be used for all sizes of the aggregate particles.
The size (100 x 100 x 510 mm) can only be used for the aggregate sizes less than 25mm. We are using this size for our test.
Average Value of MOR (fr):
There are some relationships which relate fr with compressive strength of concrete
Mean modulus of rupture is approximately 0.69√fc’ MPa
ACI code gives formulae for fr
| fr = 0.5 √ fc’ | (ACI code for Strength Calculation) | |
|
|
fr = 0.625 √ fc’ | (ACI code for Deflection Control) |
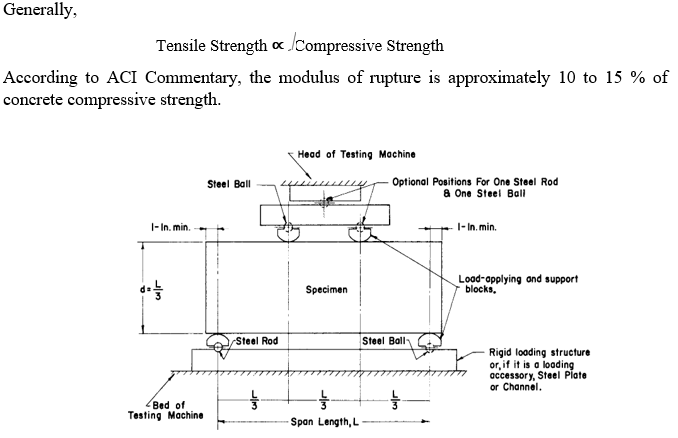
Figure showing loading arrangement of specimen in machine
Modulus of Rupture of a Prismoidal Beam:
The MOR for the test specimen can be computed by using the relation derived below;

Case — 1:
If the fracture initiates in the tension surface within the middle third of the span length, calculate the modulus of rupture as follows:
R = PL/bd2
Note: The weight of the beam is not included in the above calculation.
Case — 2:
If the fracture occurs in the tension surface outside of the middle third of the span length by not more than 5 % of the span length, calculate the modulus of rupture as follows:
R = 3Pa/bd 2
Note: The weight of the beam is not included in the above calculation.
Case — 3:
If the fracture occurs in the tension surface outside of the middle third of the span length by more than 5 % of the span length, discard the results of the test
Test specifications:
Rate of loading:
The rate of loading should be such that we get a stress of 0.02― 0.10 (MPa/s).
Acceptance Criteria of The Specimen:
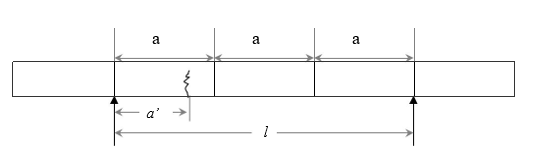
If proper compaction is not done, then the specimen may fail outside the central portion i.e.
In such a case, if;
(a – a’) > 0.05 l → Ignore the specimen and discard the results.
(a – a’) =< 0.05 l → Use the same formula but instead of a, use a’ for the calculation of MOR.
where,
a’= distance from the support center to the crack
a = one-third distance between the supports
l = distance between the supports
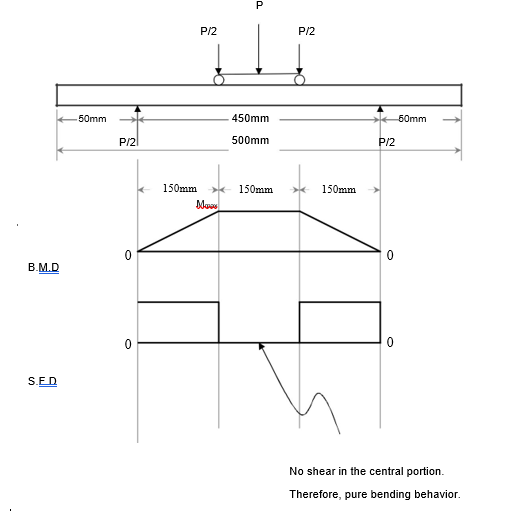
Type of loading:
The loading pattern on the beam is called the third-point/two-point loading. The main advantage of third-point loading is that, the behavior of the beam can be studied under pure bending as there is no shear at the central portion of the beam. The phenomenon is depicted by the figure below.
Procedure
When using molded specimens, turn the test specimen on its side with respect to its position as molded and center it on the support blocks. When using sawed specimens, position the specimen so that the tension face corresponds to the top or bottom of the specimen as has been cut from the parent material. Center the loading system in relation to the applied force. Bring the load-applying blocks in contact with the surface of the specimen at the third points and apply a load of between 3 and 6 % of the estimated ultimate load.
Grind, cap, or use leather shims on the specimen contact surface to eliminate any gap in excess of 0.004 in. (0.10 mm) in width. Gaps in excess of 0.015 in. (0.38 mm) shall be eliminated only by capping or grinding. Grinding of lateral surfaces should be minimized in as much as grinding may change the physical characteristics of the specimens. Capping shall be in accordance with the applicable sections of Practice C 617.
Load the specimen continuously and without shock. The load shall be applied at a constant rate to the breaking point. Apply the load at a rate that constantly increases the extreme fiber stress between 125 and 175 psi/min (0.86 and 1.21 MPa/min) until rupture occurs.
Observations & calculations
Age of specimen = 28 days
Length of beam = 500 mm
Effective length / span length of beam = 450 mm
Width of beam = 100 mm
Depth of beam = 100 mm
Supports = Simply supported beam
| Sr no. | Span length (l) | Width (b) | Depth (d) | Maximum applied load (P) | Modulus of rupture | |
| mm | mm | mm | lb | N | Mpa | |
| 1 | 450 | 100 | 100 | 1140 | 5073 | 2.2829 |
| 2 | 450 | 100 | 100 | 1160 | 5162 | 2.3229 |
| 3 | 450 | 100 | 100 | 1260 | 5607 | 2.5232 |
| Mean strength | 2.3763 | |||||
Result:
Modulus of rupture = 2.38 MPa
Comments:
- For a long time the tensile strength has been measured by means of modulus of rupture test.
- It gives indirectly tensile strength of concrete sample.
- The modulus of rupture obtained by this method is very close to the values given by double punch and split cylinder test.
Sample after the test:

